OFDM筆記-1: OFDM簡介

發表於 更新於 分類於 Disqus：

Content

分享有關OFDM的筆記。以下是OFDM筆記全系列的文章：

OFDM是什麼，能吃嗎？



  OFDM是一種基頻調變技術。像是QAM、QPSK、FSK等等，都是基頻調變技術之一。OFDM全名為「正交分頻多工」，顧名思義，就是在不同的頻率調變上訊息，而這些頻率彼此為正交。

正交 (Orthogonality)

  正交是什麼？正交就是內積為零。在一個函數空間，我們可以定義兩函數的內積，$ \langle f_1(x), f_2(x) \rangle $，為

$$
\langle f_1(x), f_2(x)\rangle = \int_I {f_1(x)f_2(x)} {\rm d}x
$$

  其中$ I $為定義的區間。類推到time domain的函數(波形)，我們可以定義兩個波形的內積為

$$
\langle F_1(t), F_2(t)\rangle = \int_{0}^{T} {F_1(t)F_2(t)} {\rm d}t
$$

  其中$ T $為symbol period。可以發現這就是一個correlator的數學式。現在，假設$ F_1(t) = \cos{2\pi f_1 t} $，$ F_2(t) = \cos{2\pi f_2 t} $，並假設$f_1 = \frac{n}{T}$，$f_2 = \frac{m}{T}$，$n$和$m$為正整數(之所以要這樣假設，是為了讓$F_1(t)$和自己的內積為$\frac{1}{2}$，$F_2(t)$亦同)。則內積$\langle F_1(t), F_2(t) \rangle$可以如下計算：

$$
\langle F_1(t), F_2(t) \rangle = \int_{0}^{T}{\cos{2\pi f_1 t}\cos{2\pi f_2 t}}{\rm d}t
$$

  使用積化合差公式得

$$
= \int_{0}^{T}{\frac{1}{2}\cos{2\pi (f_1+f_2) t}+\frac{1}{2}\cos{2\pi (f_1-f_2) t}}{\rm d}t
$$

  兩項分別積分得

$$
= \frac{1}{2}\frac{\sin{2\pi (f_1+f_2) t}}{2\pi (f_1+f_2)}\bigg{|}_{0}^{T} + \frac{1}{2}\frac{\sin{2\pi (f_1-f_2) t}}{2\pi (f_1-f_2)}\bigg{|}_{0}^{T}
$$

  繼續算你會發現第一項為零。第二項除非$f_1-f_2 = \frac{n}{2T}$，否則不為零。因此，當兩弦波滿足$f_1-f_2 = \frac{n}{2T}$，$n$為整數時，它們才會正交，而$\frac{1}{2T}$也就是這個內積下，達成正交的minimum frequency spacing。


  正交的兩個波形可以傳遞兩路的資料。因為兩者正交，在訊號空間(signal space)裡在彼此的投影量皆為零，資料的錯誤率可以降低。舉例來說，正交的M個FSK波形可以傳遞M路的資料。M-ary FSK的缺點是接收機架構比較複雜，畢竟有M個頻率的LO需要產生。

  剛才討論的是continuous time，那麼discrete time呢？當然也有正交的概念。我們可以定義discrete time domain的內積為

$$
\langle x_1[n], x_2[n]\rangle = \sum_{n=0}^{N-1} x_1[n]x_2^*[n]
$$

  其中$*$是複數共軛。現在，假設$x_1[n] = {\rm e}^{j\omega_1 n}$，$x_2[n] = {\rm e}^{j\omega_2 n}$，我們可以計算其內積：

$$
\langle x_1[n], x_2[n]\rangle = \sum_{n=0}^{N-1} {\rm e}^{j(\omega_1-\omega_2) n}
$$

  用級數和的公式得到

$$
= \frac{1-{\rm e}^{j(\omega_1-\omega_2) N}}{1-{\rm e}^{j(\omega_1-\omega_2)}}
$$

  此式等於零的情況發生於$\omega_1-\omega_2 = \frac{2\pi m}{N}$，其中$m$為整數。換句話說，在discrete time的case，符合正交特性的minimum frequency spacing為$\frac{2\pi}{N}$。


  其實這個結果可以從continuous time的結果推得。假設我們將continuous time的波形以$\frac{N}{T}$的取樣頻率取樣，則在$T$的週期可以取得$N$個samples，正好就是我們discrete time的訊號。由取樣定裡得知，$\frac{1}{2T}$經取樣變成discrete time的頻率，$2\pi\cdot\frac{1/2T}{f_s} = \frac{\pi}{N}$。


  怎麼算出來不一樣？事實上在continuous time的case中，如果用complex sinusoid來算，就會算出一樣的結果(minimum spacing = $\frac{1}{T}\rightarrow\frac{2\pi}{N}$)。之所以會發生這種事，是因為當我們只考慮real function(也就是餘弦波$\cos(x)$)，求出來反導函數$\sin(x)$有兩個零點$x = \{0,-\pi\}, x\in[-\pi, \pi)$，而當我們考慮complex sinusoid，求出來的反導函數$1 - {\rm e}^{jx}$只有一個零點$x = 0, x\in[-\pi, \pi)$。

分頻多工 (Frequency-Division Multiplexing)

  不同的頻率可以拿來傳輸不同的資料，這就是分頻多工。其實分頻多工不只在OFDM，在其他通訊技術也有相當的應用，如第三代無線通訊系統WCDMA使用的FDD，就是透過分頻來實現雙工。


  那麼OFDM的頻率分工有什麼特別的呢？OFDM在彼此正交的子載波上進行分工，而且相鄰subchannel重疊，因此和一般頻率分工相比，OFDM的頻寬使用效率(bandwidth efficiency)較高。下面這個影片說明的很清楚，OFDM將symbol duration拉長，減少ISI的影響，更透過子載波間正交的特性，消除ICI。


OFDM的運作方式？

  OFDM的運作簡單來說就是：

  • 將bits map到星座圖，以串列資料的方式送到運算單元。
  • 將串列資料轉為並列資料。
  • 將並列資料做IFFT轉換，N個並列資料使用N-point IFFT。
  • N-point IFFT的並列輸出改為串列輸出。
  • 加上cyclic prefix，形成一個OFDM symbol。
  • samples經過濾波、DAC後便送到射頻前端，準備傳送！

  下面這張圖簡單呈現這個流程。


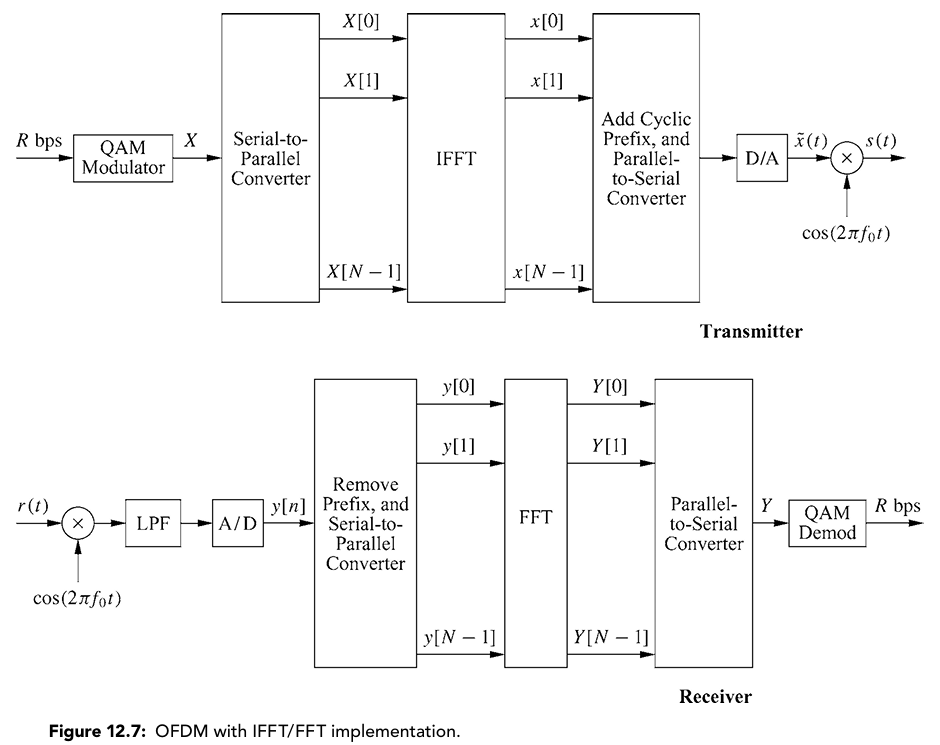
OFDM block diagram. Source: Fig. 12.7, 12.4.3 in [1].

  由於OFDM是以數位調變的方式運作，受惠於VLSI技術的發展，IFFT、FFT、串列轉並列、並列轉串列可以使用數位IC來實現，降低生產成本，因此被廣泛使用。接著便詳細介紹OFDM的訊號處理、收發機架構。

訊號處理

  以下就來介紹OFDM的訊號處理方法。前面提到過，第一步是將bits map到星座圖上，比如說QPSK就是兩個bits對應到星座圖上的一個點，64QAM就是六個bits對應到一個點。下表整理出OFDM在不同通訊技術中使用到的星座圖(參考自[3]，[4]，[5]，[6])。


技術 星座圖 說明
DVB-T QPSK, 16QAM, 64QAM 配合high-priority bits的使用，還有non-uniform的16QAM和64QAM
DVB-T2 同上，加上256QAM 不再使用DVB-T的two hierarchy levels
LTE-advanced QPSK, 16QAM, 64QAM, 256QAM 即所謂的4G行動通訊技術
5G NR BPSK, QPSK, 64QAM, 256QAM 5G NR也採用NOMA等非正交的技術
802.11n BPSK, QPSK, 16QAM, 64QAM Wi-Fi 4，引用MIMO技術
802.11ax 同上，加上256QAM，1024QAM Wi-Fi 6，1024QAM也太龐大

  轉換為星座圖上的點後，要將每個點調變到子載波(subcarrier)上。怎麼做呢？使用Discrete Fourier Transform (DFT)。下面複習一下DFT的基本性質：

$$
\begin{align}
&X[k] = \sum_{n = 0}^{N - 1}{x[n] W_{N}^{kn}} \\[10pt]
&x[n] = \frac{1}{N} \sum_{k = 0}^{N - 1}{X[k] W_{N}^{-kn}} \\[10pt]
&x[(n - m)\text{ mod }N] \longleftrightarrow W_{N}^{km} X[k]\quad\text{(circular shift)} \\[10pt]
&X[n] \longleftrightarrow Nx[(-k)\text{ mod }N]\quad\text{(duality)}
\end{align}
$$

  還有與circular convolution相關的性質：

$$
\begin{align}
&x_1[n]\ \enclose{circle}{N}\ x_2[n] = \sum_{m = 0}^{N - 1}{x_1[m] x_2[(n - m)\text{ mod }N]},\quad 0 \leq n \leq (N - 1)\\[10pt]
&x_1[n]\ \enclose{circle}{N}\ x_2[n] = x_2[n]\ \enclose{circle}{N}\ x_1[n]\quad\text{(commutative)}\\[10pt]
&x_1[n]\ \enclose{circle}{N}\ x_2[n] \longleftrightarrow X_1[k] X_2[k]\\[10pt]
&x_1[n] x_2[n] \longleftrightarrow \frac{1}{N} X_1[k]\ \enclose{circle}{N}\ X_2[k]\quad\text{(from duality)}
\end{align}
$$

  其中 $W_{N} = e^{-j\frac{2\pi}{N}}$。


  假設N個星座點 $a_k$ (複數)，分別調變到N個子載波 $\phi_k[n] = \rm e^{j\frac{2\pi}{N} kn},\quad 0 \leq n \leq (N - 1)$，則第k個子載波的訊號為 $a_k\phi_k[n]$ (其實只是相乘)，全部子載波訊號加起來為

$$
\begin{align}
x[n] &= \sum_{k = 0}^{N - 1}{a_k\phi_k[n]}\\[10pt]
&= \sum_{k = 0}^{N - 1}{a_k W_{N}^{-kn}}
\end{align}
$$

  上面的式子就是IDFT，不過少了 $1/N$ 的常數。也就是說，將並列送來的N個星座點作IDFT運算，得到的就是時域的訊號波形。到這裡為止都是discrete time的訊號，因此之後還要經過濾波器(或是windowing)、DAC轉換為類比波形，才是可以傳送的訊號。典型的OFDM頻譜如下圖。


OFDM頻譜示意圖。圖片來源：yatebts.com，連結

  為什麼每個子載波的頻譜是sinc函數呢？原因是我們剛才假設將星座點調變到子載波的方式為相乘：

$$
\begin{align}
&a_k\phi_k[n] = a_k\Pi[n]\phi_k[n]\\[10pt]
&\Pi[n] =
\begin{cases}
1,\quad 0 \leq n \leq (N - 1)\\
0,\quad \text{otherwise}
\end{cases}
\end{align}
$$

  可以知道調變過程中，我們採取的pulse function為方波，因此在頻域會呈現sinc函數。若經過濾波器則調變波形不再是方波，頻域也不會是sinc函數。


  實務上，OFDM會使用IFFT來實現IDFT、FFT實現DFT，不過FFT只是實現DFT的演算法，和DFT的性質沒有太大關係，所以這裡就不介紹。

  話不多說，直接跑模擬看看吧！生成資料、轉換為星座點(這裡以BPSK為例)，再轉換為時域波形。這裡使用zero-padding的技巧，來逼近連續的波形。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
% --- parameter settings --- %
Nb = 64; % number of bits
fs = 1000; % sampling frequency
oversampling = 100; % zero-padding factor

% --- Tx --- %
b = 2 * round(rand(1, Nb)) - 1; % generate transmit information bits
s = ifft((Nb * oversampling) * b, Nb * oversampling); % IDFT

% --- presentation --- %
t = (0: Nb * oversampling - 1) / fs / oversampling;
plot(t, real(s), "-b", "LineWidth", 2);
xlim([0.003 t(0.6 * Nb * oversampling)]);
xlabel("time (seconds)", "FontName", "Times New Roman");
ylabel("{\bf{Re}}\{s(t)\}", "FontName", "Times New Roman", "interpreter", "latex");

clear

  下圖是模擬出來的時域波形，可以看到OFDM的主要問題之一，就是瞬時功率變化劇烈，相較於其他調變方式，有較高的PAPR(Peak-to-Average Power Ratio)。


MATLAB模擬OFDM波形。

收發機架構

  OFDM經典的收發機架構如下圖所示。


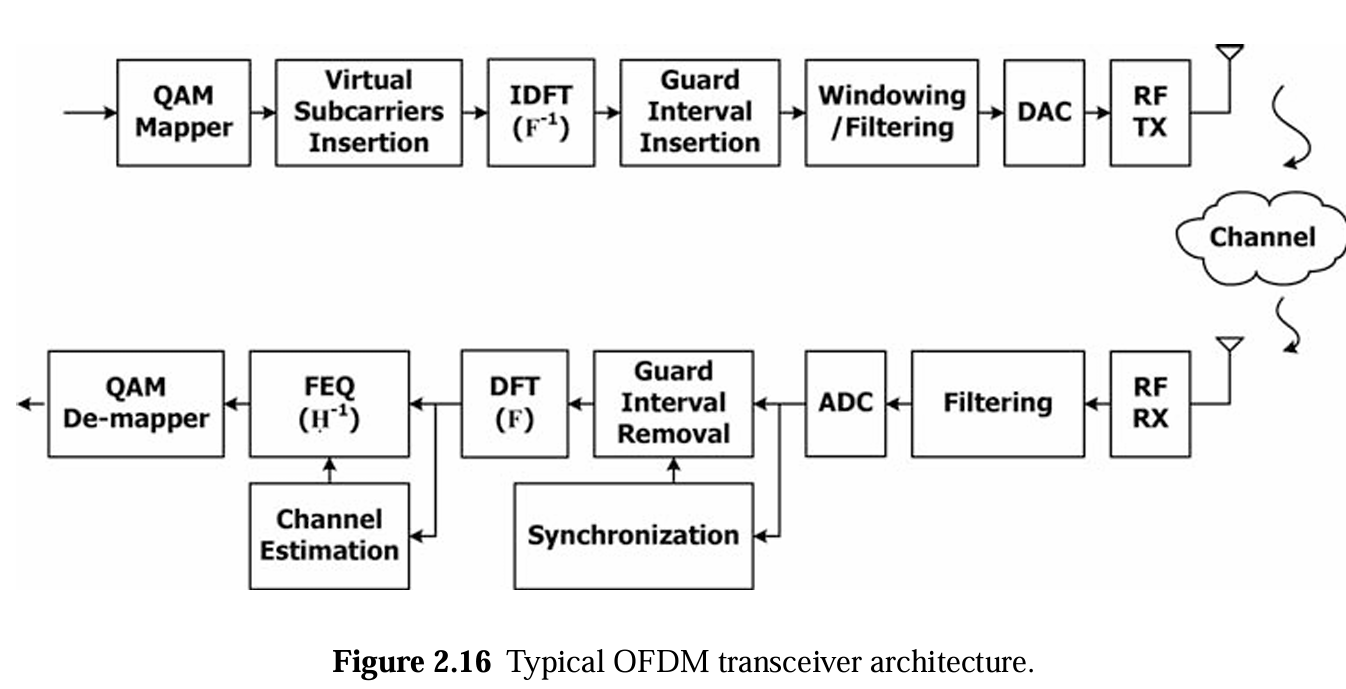
OFDM transceiver architecture. Source: Fig. 2.16, 2.2.3 of [2].

  和剛才的block diagram很像，不過多了CP (cyclic prefix)，後面會簡單介紹CP的作用。

  也來跑模擬試試看吧！此程式中，模擬了從產生symbol、IFFT、CP、channel一直到Rx的過程，也計算出SER以驗證模擬的正確性。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
% ----- parameters setting ----- %
Nb = 6e7; % number of transmitted bits
Nsubc = 64; % number of OFDM subcarriers
Pcp = 1 / 8; % proportion of CP length to OFDM sym duration
SNR = 10 .^ (0.1 * (0: 12)); % SNR = Es/N0 (linear scale)
N0  = 1;% single-sided psd of AWGN
channel_length = 9;
Mod = 1;% modulation type
        % 1 -> BPSK
        % 2 -> QPSK
        % 3 -> 16QAM
        % 4 -> 64QAM
mod_types = ["BPSK", "QPSK", "16QAM", "64QAM"]; % modulation types

rng();
bits = round(rand(1, Nb)); % transmitted information

% ----- channel setting ----- %
PDP = [0.0 -1.1 -2.2 -3.3 -4.3 -5.4 -6.5 -7.6 -8.7 -9.8 ...
       -10.9 -11.9 -13.0 -14.1 -15.2 -16.3 -17.4 -18.5 -19.5]; % Power Delay Profile (dB)
h = sqrt(0.5 * 10 .^ (0.1 * PDP(1: channel_length))) .* (randn(1, channel_length) + 1j * randn(1, channel_length)); % TGac CIR
H = fft(h, Nsubc); % channel gain for each subcarrier

% ----- run simulation ----- %
BER = zeros(1, length(SNR));
BER_theo = zeros(1, length(SNR));
for snr = SNR
    
    % ----- Transmitter ----- %
    X = bit2sym(bits, Mod, snr * N0);
    Nsym = round(length(X) / Nsubc); % number of OFDM symbols
    X = reshape(X, [Nsubc, Nsym]);
    x = ifft(X, [], 1); % ifft along each row
    xc = [x(end - round(Pcp * Nsubc) + 1: end, :); x]; % adding CP
    xc = reshape(xc, [1, Nsym * round((1 + Pcp) * Nsubc)]);

    % ----- Channel ----- %
    xr = conv(xc, h);
    xr = xr + sqrt(N0 / 2 / Nsubc) * (randn(1, length(xr)) + 1j * randn(1, length(xr)));

    % ----- Receiver ----- %
    xr = xr(1, 1: end - length(h) + 1); % remove the (useless) tail
    xr = reshape(xr, [round((1 + Pcp) * Nsubc), Nsym]);
    y = xr(round(Pcp * Nsubc) + 1: end, :); % removing CP
    Y = fft(y, [], 1); % fft along each row
    Y = Y .* (1 ./ H).'; % one-tap equalization
    Y = reshape(Y, [1, Nsym * Nsubc]);
    bits_r = sym2bit(Y, Mod, snr * N0); % recovered (decoded) bits
    
    % ----- BER calculation ----- %
    BER(SNR == snr) = 1 - sum(bits_r == bits) / Nb;
    BER_theo(SNR == snr) = theoBER(snr * abs(H) .^ 2, Mod);

end

% ----- plot BER ----- %
fig = figure();
semilogy(10 * log10(SNR), BER_theo, "-rdiamond", "LineWidth", 2.5);
grid on; hold on
semilogy(10 * log10(SNR), BER, "-bdiamond", "LineWidth", 2.5);
legend("theo", "sim");
scale_control = 10 ^ floor(log10(BER_theo(end)));
xlim([0 12]); ylim([scale_control 1]);
title(sprintf("BER of OFDM, static channel, mod = %s", mod_types(Mod)));
xlabel("SNR (E_b/N_0) (dB)"); ylabel("Bit Error Rate (BER)");
fontname("Times New Roman"); fontsize(fig, 14, "points");

% ----- plot channel chain ----- %
fig = figure();
stem(-Nsubc / 2: Nsubc / 2 - 1, abs(fftshift(H)), "^", "MarkerFaceColor", "cyan");
title("channel gain for each subcarrier");
xlabel("index (k)"); ylabel("$\vert H_k\vert$", "Interpreter", "latex");
fontname("Times New Roman"); fontsize(fig, 14, "points");

% ----- plot channel impulse response ----- %
fig = figure();
stem(0: length(h) - 1, abs(h), "MarkerFaceColor", "b");
title("channel impulse response");
xlabel("index (n)"); ylabel("$\vert h[n]\vert$", "Interpreter", "latex");
fontname("Times New Roman"); fontsize(fig, 14, "points");

clear

  其中用到的函數定義如下(MATLAB的話應該是可以善用toolbox的，這裡我只用到Communications Toolbox的 qammod 和 qamdemod，因為64QAM的bit mapping實在是太龐雜)：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
function S = bit2sym(b, opt, Eb)
% map bits to freq-domain symbols
% b   -> input bits
% Eb  -> average bit energy
    
    if opt == 1
        % --- BPSK --- %
        S = sqrt(Eb) * (2 * b - 1);
    elseif opt == 2
        % --- QPSK --- %
        b = reshape(b, [2, round(length(b) / 2)]);
        S = sqrt(Eb) * (2 * b(1, :) - 1 + 2j * b(2, :) - 1j);
    elseif opt == 3
        % --- 16QAM --- %
        % --- using Gray code --- %
        b = reshape(b, [4, round(length(b) / 4)]);
        S = sqrt(4 * Eb / 10) * ((1 - 2 * b(2, :)) .* (1 + 2 * b(4, :)) + ...
                        1j * ((1 - 2 * b(1, :)) .* (1 + 2 * b(3, :))));
    elseif opt == 4
        % --- 64QAM --- %
        % --- using qammod from Communications Toolbox --- %
        b = reshape(b, [6, round(length(b) / 6)]);
        S = bits2dec(b, 6);
        S = sqrt(6 * Eb / 42) * qammod(S, 64, "gray");
    end
end

function b = sym2bit(S, opt, Eb)
% map freq-domain symbols to bits (detection at Rx)
% S   -> input symbols
% Eb  -> average bit energy

    if opt == 1
        % --- BPSK --- %
        b = real(S) > 0;
    elseif opt == 2
        % --- QPSK --- %
        b = [real(S) > 0; imag(S) > 0];
        b = reshape(b, [1, 2 * length(S)]);
    elseif opt == 3
        % --- 16QAM --- %
        b = [imag(S) < 0; real(S) < 0; abs(imag(S)) > 2 * sqrt(4 * Eb / 10); abs(real(S)) > 2 * sqrt(4 * Eb / 10)];
        b = reshape(b, [1, 4 * length(S)]);
    elseif opt == 4
        % --- 64QAM --- %
        % --- using qamdemod from Communications Toolbox --- %
        S = qamdemod(S / sqrt(6 * Eb / 42), 64, "gray");
        b = dec2bits(S, 6);
        b = reshape(b, [1, 6 * length(S)]);
    end
end

function ber = theoBER(snr, opt)
% calculate theoretical BER
% snr -> Eb/N0, Eb is the average bit energy
    
    if opt == 1
        % --- BPSK --- %
        ber = mean(0.5 * erfc(sqrt(snr)));
    elseif opt == 2
        % --- QPSK --- %
        ber = 0.5 * mean(1 - (1 - 0.5 * erfc(sqrt(snr))) .^2);
    elseif opt == 3
        % --- 16QAM --- %
        % --- union bound --- %
        ber = 3 * mean(0.5 * erfc(sqrt(4 * snr / 10))) / 4;
    elseif opt == 4
        % --- 64QAM --- %
        % --- union bound --- %
        ber =  (224 / 64) * mean(0.5 * erfc(sqrt(6 * snr / 42))) / 6;
    end
end

function d = bits2dec(b, N)
% convert bit vectors to corresponding decimal values
% N -> number of bits
    
    d = zeros(1, length(b));
    for k = 0: N - 1
        d = d + 2 ^ (N - k - 1) * b(k + 1, :);
    end
end

function b = dec2bits(d, N)
% convert decimal vector to binary ones
% N -> number of bits
    
    b = zeros(N, length(d));
    for k = N - 1: -1: 0
        b(N - k, :) = floor(d / 2 ^ k);
        %b(N - k, :) = bitshift(d, -k);
        d = d - 2 ^ k * floor(d / 2 ^ k);
    end
end

  下圖是OFDM BPSK的SER (= BER)，比一般的BPSK錯誤率還要高，這是因為每個子載波遭遇的通道增益(channel gain，即 $H[k]$)不一樣，較小的通道增益會導致較高的錯誤率。圖中的SER即是將各個子載波的SER平均而得。


  (2025/12/30編按：上述的程式沒有對channel的impulse response做normalization，這會使得接收機接收到的平均SNR異於AWGN only的SNR，因此下圖的錯誤率對照到的SNR是錯誤的。)


OFDM BPSK錯誤率，使用上列程式裡的通道。

Cyclic Prefix

  剛才的模擬中，我們在time-domain samples加入了cyclic prefix (CP)，它有什麼作用呢？首先，要知道在多路徑通道(multipath channel)中，相鄰的OFDM symbol會因為延遲而互相干擾，稱為ISI (inter-symbol inteference)，相鄰OFDM symbol不同子載波間也會形成干擾，稱為ICI (inter-carrier inteference)。CP可以作為相鄰OFDM symbol之間的guard interval，避免ISI和ICI的產生。

  除此之外，CP還可以用來對抗多路徑通道。假設一個static channel (LTI系統)，通道脈衝響應為 $h[n]$，長度為 $L$，並且假設CP長度為 $N_{CP} < L$。則OFDM symbol (useful part) + CP和 $h[n]$ 做linear convolution，等同於OFDM symbol (useful part)和 $h[n]$ 做circular convolution！這有什麼了不起嗎？有的，前面提過下面的關係式：

$$
x_1[n]\ \enclose{circle}{N}\ x_2[n] \longleftrightarrow X_1[k] X_2[k]
$$

  故

$$
x[n]\ \enclose{circle}{N}\ h[n] \longleftrightarrow X[k] H[k]
$$

  其中 $H[k]$ 為 $h[n]$ 的N-point DFT。這表示我們將接收到的time domain sample做DFT後，對每一個subcarrier的投影量 $Y[k] = X[k] H[k]$ 乘上 $1/H[k]$，便可以還原回原本的符號，此即one-tap equalization。

  CP還可以拿來處理STO、CFO的問題。之後再寫一篇來更詳細的介紹CP。(這就是我嗑的CP！)

哪裡會用到OFDM？

  OFDM最早是使用filter bank來實現，並且用於voiceband communication。由於filter bank的成本高、設計困難，一開始OFDM並不受重視。後來OFDM使用在DSL/ADSL (Digital Subscriber Loop)，即貝爾實驗室的Cioffi和Amanti設計的DMT (Digital Multi-Tone)。[7]這篇文章介紹了OFDM的歷史，作者是當年和其他人共同提出使用FFT來實現OFDM的貝爾實驗室工程師，可以說是OFDM廣泛應用的推手。


  現在使用到OFDM的技術有：WiFi、WiMAX、LTV advanced、5G NR等等，在光纖通訊也有應用。不過隨著5G開始採用NOMA等非正交的調變方式，可以預期傳統的OFDM必然迎來改變，或是衍生其他的技術。

OFDM的變體？

DMT

  一直以為大學時數位通訊模擬的是OFDM，最近瀏覽過去寫的程式，才發現原來當初是模擬DMT(至少講義裡是寫DMT)。這篇文章簡單說明了DMT和OFDM的異同之處。簡單來說：

DMT就是一種OFDM！

  在前一節也提到，DMT是最早以FFT實現OFDM的調變方式之一，主要用於ADSL。所以OFDM比較像是一個概念，DMT則是實現OFDM的實體層調變方式。

OFDMA

  參考[8]，OFDMA和OFDM的差異主要在於，傳統的OFDM系統多重存取(multiple access)資源的方式為分時存取，也就是不同時槽可以提供不同使用者使用；而OFDMA則是在頻域也劃分出好幾個RE (resource element)，在時域和頻域的劃分便形成好幾個RB (resource block)，分配給不同使用者使用。

SC-FDMA

  參考[9]，全名為Single-Carrier FDMA，也就是單載波的「頻率多重存取」，好像有些矛盾？單載波要怎麼做到多重存取？參考下圖，SC-FDMA的系統方塊圖和OFDM相當相似，只差在SC-FDMA裡，符號其實是在時域表示。時域的符號N個為一組，經過DFT轉換到頻域後，再把這N點分配給M個子載波裡的N個一組；接著，下一組時域符號再依此處裡。


SC-FDMA的系統方塊圖。

  也就是說，每一組時域符號可以提供給一個使用者，而且同時間M個子載波只會承載一個使用者的資料(儘管有些子載波承載的是零)；因此，SC-FDMA不是在頻率多重存取，而是在時間上多重存取。那為什麼還可以稱作FDMA？因為一個使用者使用的子載波頻率不一定相同，有點像是跳頻的概念，雖然這也不算是multiple access…。

結語

  結果這篇文章竟然花了六個月 aka 半年才寫好？原本是打算進實驗室前就把OFDM的東西看完，結果拖延症如常發作，竟然拖到現在…。OFDM是前幾個世代行動通訊(e.g. 4G)和WLAN (e.g. Wifi)的重要基礎，雖然自5G開始出現了其他候選技術，OFDM作為經典的調變方式，依然值得通訊領域的研究生學習、分析。

參考資料

[1] A. Goldsmith, Wireless Communications. Cambridge University Press, 2005.

[2] T.D. Chiueh, et al, Baseband Receiver Design for Wireless MIMO-OFDM Communications. John Wiley & Sons Singapore Pte. Ltd, 2012.

[3] ETSI EN 300 744 v1.6.1. Digital Video Broadcasting (DVB): Framing structure, channel coding and modulation for digital terrestrial televisio, 2009.01. Available: https://www.etsi.org/deliver/etsi_en/300700_300799/300744/01.06.01_60/en_300744v010601p.pdf

[4] 交通部電信總局(NCC前身)委託的計畫報告。李學智等，
數位無線地面電視單頻網建置技術之分析與研究期末報告，2004.10。Available: https://www.ncc.gov.tw/chinese/files/07051/474_963_070517_1.pdf

[5] ETSI TS 138 211 V16.2.0. 5G NR: Physical channels and modulation, 2020.07. Available: https://www.etsi.org/deliver/etsi_ts/138200_138299/138211/16.02.00_60/ts_138211v160200p.pdf

[6] Wi-Fi 6, Wikipedia. Available: https://en.wikipedia.org/wiki/Wi-Fi_6

[7] S. B. Weinstein, “The history of orthogonal frequency-division multiplexing [History of Communications],” in IEEE Communications Magazine, vol. 47, no. 11, pp. 26-35, November 2009. Available: https://ieeexplore.ieee.org/document/5307460/similar#similar

[8] 網站 LTE筆記: SC-FDMA vs. OFDMA (1)

[9] 網站 LTE筆記: SC-FDMA vs. OFDMA (2)