有關FFT的一些問題釐清

發表於 分類於 Disqus：

What?

  FFT是非常重要的數值運算技術，讓OFDM技術得以實現。在吳炳飛教授的數位訊號處理講義裡，提到FFT的butterfly運算結構，並且畫了下圖(圖A)，來說明butterfly結構可以如何化簡。


圖A，兩個stage之間的運算結構。改自講義。

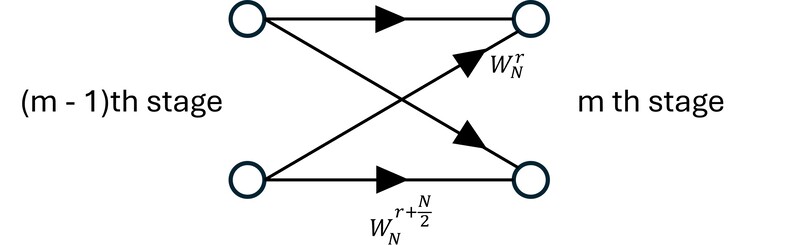
  化簡後就會長成如圖B的樣子。當中只出現了一個complex exponential( $W_{N}^{r}$ )，因此也可以減少硬體(如暫存器)的使用。


圖B，再化簡後的運算結構。改自講義。

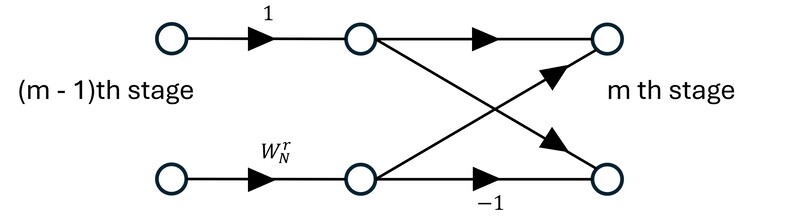
  但是圖A和圖B是怎麼來的？講義裡以N = 8(N為FFT點數)作為例子，可不可以用更一般化的方式來理解？這篇文章就要來釐清這個問題。

Explanation

  開始碰數學吧。假設有一個長度為 $N$ 的訊號(samples)，我們對它做 $N$-point DFT來了解頻譜資訊。

$$
X[k] = \sum_{n = 0}^{N - 1}{x[n]W_N^{kn}},\quad 0 \leq k \leq N - 1
$$

  其中 $W_N^{k} = e^{-j\frac{2\pi}{N}k}$。假設 $N$ 為2的冪次，即 $N = 2^{\nu}$，因此 $N$ 也是偶數。則剛才的式子可以拆成兩項：n為偶數的samlpes和n為奇數的samples：

$$
\begin{align}
X[k] &= \sum_{n\ even}{x[n]W_N^{kn}} + \sum_{n\ odd}{x[n]W_N^{kn}}\\[10pt]
&= \sum_{l = 0}^{\frac{N}{2} - 1}{x[2l]W_N^{2lk}} + \sum_{l = 0}^{\frac{N}{2} - 1}{x[2l + 1]W_N^{(2l + 1)k}}\\[10pt]
&= \sum_{l = 0}^{\frac{N}{2} - 1}{x[2l]W_{\frac{N}{2}}^{lk}} + W_N^k \sum_{l = 0}^{\frac{N}{2} - 1}{x[2l + 1]W_{\frac{N}{2}}^{lk}}\\[10pt]
&= X_{0}[k] + W_N^{k}X_{1}[k]
\end{align}
$$

  $X_{0}[k]$ 為n為偶數的samples做出來的 $N/2$-point DFT，$X_{1}[k]$ 為n為奇數的samples做出來的 $N/2$-point DFT。下標0表示偶數，1表示奇數，之後會發現這相當的好用。從上面的式子還可以發現一件事：

$$
\begin{align}
X[k + \frac{N}{2}] &= X_{0}[k + \frac{N}{2}] + W_N^{k + \frac{N}{2}}X_{1}[k + \frac{N}{2}]\\[10pt]
&= X_{0}[k] - W_N^{k}X_{1}[k],\quad 0 \leq k \leq \frac{N}{2} - 1
\end{align}
$$

  也就是說 $X[k]$ 和 $X[k + \frac{N}{2}]$ 用到的是前一個stage的同一組結果，只不過係數稍有不同(就差一個負號)。以此類推，就可以把DFT運算簡化為butterfly的結構，運算複雜度從原本的 $O(N^2)$ 變為 $O(N\lg{N})$，此即FFT的強大之處。(這裡使用的是Decimation in Time, DIT的方法。)


  剛才我們將DFT增加一階來化簡，還可不可以再化簡？當然可以！怎麼做？把偶數index的部分再分為偶數和奇數就行了，如下：

$$
\begin{align}
X_0[k] &= \sum_{l = 0}^{\frac{N}{2} - 1}{x[2l]W_{\frac{N}{2}}^{kl}}\\[10pt]
&= \sum_{l\ even}{x[2l]W_{\frac{N}{2}}^{kl}} + \sum_{l\ odd}{x[2l]W_{\frac{N}{2}}^{kl}}\\[10pt]
&= \sum_{r = 0}^{\frac{N}{4} - 1}{x[4r]W_{\frac{N}{2}}^{2rk}} + \sum_{r = 0}^{\frac{N}{4} - 1}{x[4r + 2]W_{\frac{N}{2}}^{(2r + 1)k}}\\[10pt]
&= X_{(0,0)}[k] + W_N^{2k}X_{(1,0)}[k]
\end{align}
$$

  下標的部分，$(0,0)$ 表示偶數index中再取偶數index，$(1,0)$ 表示偶數index中再取奇數index，要從右往左看。對於 $X_1[k]$，如法炮製(過程就省略了)：

$$
X_1[k] = X_{(0,1)}[k] + W_N^{2k}X_{(1,1)}[k]
$$

  所以 $X[k]$ 可以表示為

$$
\begin{align}
X[k] &= X_{(0,0)}[k] + W_N^{2k}X_{(1,0)}[k] + W_N^k(X_{(0,1)}[k] + W_N^{2k}X_{(1,1)}[k])\\[10pt]
&= X_0[k] + W_N^{2k}X_2[k] + W_N^kX_1[k] + W_N^{3k}X_3[k]
\end{align}
$$

  上面的式子裡，把下標從二進位改為十進位表示，比如說 $(1,0) \rightarrow 2$。好像有點複雜？確實，不過從上面的式子可以看出兩點：

  1. 繼續化簡下去的話，就是DFT原本的表示式，因為化簡到最後的 $X_{(\cdots)}[k]$ 就是time-domain samples本身。所以化簡動作本身並沒有讓我們計算更方便，而是化簡過程中，發現使用到重複的項(比如說剛才的 $X[k]$ 和 $X[k + \frac{N}{2}]$)，才使得運算複雜度降低。(有點動態規劃的Fu？)

  2. 假設在某個stage m我有一個node $X_{d}[k]$，這個node一定可以再分為前一個stage的兩個node(除非已經是time-domain samples了)。沒有什麼理論依據，就是做得到。


  接著我們就把它一般化為mth stage和(m - 1)th stage的關係，以證實圖A和圖B的正確性。首先我們要定義stage，如下圖，time-domain samples定義為0th stage，而最後的DFT結果($X[k]$)定義為$\nu$th stage。


圖C，FFT butterfly結構的stage定義。

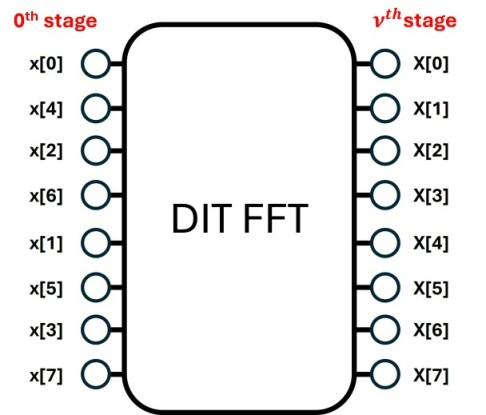
  現在，來看看mth stage的某個node，$X_d[k]$。這裡的 $d$ 是一個 $(\nu - m)$ bits的數字，也就是說 $d$ 介於 $0 \sim (2^{\nu - m} - 1)$ 之間。由於是在mth stage，已經經過 $(\nu - m)$ 次簡化，因此它是一個 $N/2^{\nu - m} = 2^m$-point DFT的結果，可以寫成下面這個樣子($N’ = 2^m$)：

$$
X_d[k] = \sum_{i = 0}^{N’ -1}{g[i]W_{N’}^{ki}}
$$

  $g[i]$ 是根據某個規則從x[n]挑出來的samples。和剛才的作法一樣，分為偶數index和奇數index：

$$
\begin{align}
X_d[k] &= \sum_{i\ even}{g[i]W_{N’}^{ki}} + \sum_{i\ odd}{g[i]W_{N’}^{ki}}\\[10pt]
&= \sum_{j = 0}^{\frac{N’}{2} - 1}{g[2j]W_{N’}^{2kj}} + \sum_{j = 0}^{\frac{N’}{2} - 1}{g[2j + 1]W_{N’}^{(2j + 1)k}}\\[10pt]
&= \sum_{j = 0}^{\frac{N’}{2} - 1}{g[2j]W_{\frac{N’}{2}}^{kj}} + W_{N’}^k\sum_{j = 0}^{\frac{N’}{2} - 1}{g[2j + 1]W_{\frac{N’}{2}}^{kj}}\\[10pt]
&= X_{d’}[k] + W_{N’}^kX_{d’’}[k] \tag{1}
\end{align}
$$

  當中，$d’$ 和 $d’’$ 為 $(\nu - m + 1)$ bits的數字。$d’$ 的數值和 $d$ 相同，只不過多一個digit，MSB為0；$d’’ = d + 2^{\nu - m}$，MSB為1。因為 $X_{d’}[k]$ 和 $X_{d’’}[k]$ 都是 $\frac{N’}{2}$ - periodic，可以得知

$$
\begin{align}
X_d[k + \frac{N’}{2}] &= X_{d’}[k + \frac{N’}{2}] + W_{N’}^{k + \frac{N’}{2}}X_{d’’}[k + \frac{N’}{2}]\\[10pt]
&= X_{d’}[k] - W_{N’}^kX_{d’’}[k] \tag{2}
\end{align}
$$

  式(1)和式(2)是不是有些似曾相識？畫成圖如下，原來它就是圖B。這證實圖A和圖B的正確性，也說明mth stage和(m - 1)th stage之間的關係。


圖D，兩個stage之間的關係。

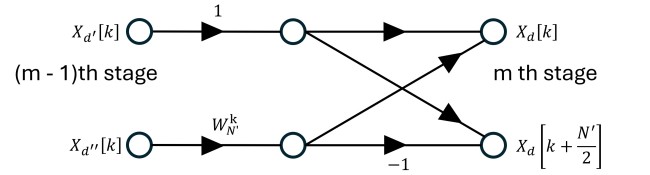
  從式(1)也可以看得出來，在1st stage，也就是time-domain samples做2-point DFT的階段，若上方的sample為 $x[d’] = x[d]$，則同一組下方的sample為 $x[d’’] = x[d + 2^{\nu - 1}] = x[d + \frac{N}{2}]$。

Complexity

  雖然這不是我原本的問題，不過也把思考的過程記錄下來。沒有使用DIT FFT演算法前，$N$-point DFT的複數乘法量($m$)為$N^2$，複數加法量($a$)為$N^2 - N$。以 $S$ 表示化簡成幾個stage，如下(係數為-1也算乘法)：

  • $S = 1$，就是沒有化簡，$m = N^2$，$a = N^2 - N$。
  • $S = 2$，$m = 2\times(\frac{N}{2})^2 + N$，$a = 2\times\frac{N}{2}(\frac{N}{2} - 1) + N$。
  • $S = 3$，$m = 2\times(2\times(\frac{N}{4})^2 + \frac{N}{2}) + N$，$a = 2\times(2\times\frac{N}{4}(\frac{N}{4} - 1) + \frac{N}{2}) + N$。

  看起來可以表達成遞迴式。令 $m(i)$ 表示計算i-point DIT FFT所需的複數乘法量，$a(i)$ 表示所需的複數加法量，則：

$$
\begin{align}
m(i) &= 2\cdot m(\frac{i}{2}) + i\\[10pt]
a(i) &= 2\cdot a(\frac{i}{2}) + i
\end{align}
$$

  因為 $m(4) = 12$，$a(4) = 8$，可以推得($N = 2^{\nu}$)：

$$
\begin{align}
m(2^\nu) &= 2^{\nu - 2}\cdot 12 + (\nu - 2)2^{\nu}\\[10pt]
&= (\nu + 1)2^{\nu},\quad \nu \geq 3\\[10pt]
&= N(\lg{N} + 1)\\[10pt]
a(2^\nu) &= 2^{\nu - 2}\cdot 8 + (\nu - 2)2^{\nu}\\[10pt]
&= \nu2^{\nu},\quad \nu \geq 3\\[10pt]
&= N\lg{N}
\end{align}
$$

  上面的式子假設係數為-1也算是乘法；如果不算的話，複數乘法量還可以再減少，不過只是相乘的常數減少，複雜度還是 $O(N\lg{N})$。

參考資料

  本文參考吳炳飛教授的數位訊號處理講義。