無線通道介紹-1:通道模型簡介
Content
今年(2025)開始對無線通道有一些初步的了解,將筆記記錄在這裡。
以下是無線通道介紹的全系列文章:
通訊通道543
在通訊技術的發展歷史中,無線與有線的競爭非常精彩。最早使用電能的通訊技術是有線的(當然飛鴿傳書不算)──西元 1837 年 Morse 發明摩斯密碼,電報系統開創現代通訊的紀元;西元 1895 年,Marconi 發明無線電報傳輸,是為無線通訊的濫觴。自此以後,通訊技術便在有線與無線的方式之間擺盪:二十世紀初,電話網路系統 PSTN (有線)逐漸形成,同時 AM 和 FM 無線電廣播(無線)也蓬勃發展。
戰後無線電視與有線電視互別苗頭,同時隨著電腦間通訊的需求出現,1970 年代的 ARPANET (有線)和 ALOHA 網路(無線)開啟了接下來五十年的技術大躍進──Ethernet (有線)、AMPS (無線)、光纖傳輸(有線)及行動通訊(無線)輪番上陣,形成現在的局面。
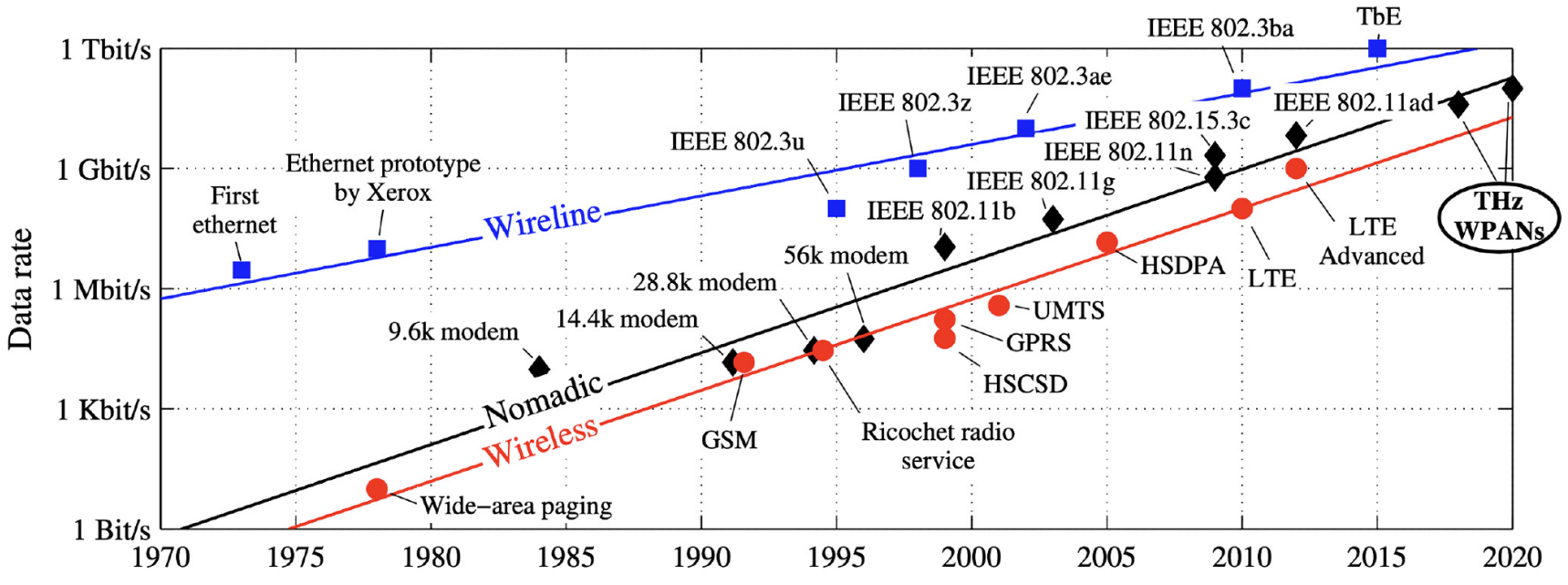
圖片來源:Terahertz Integrated Circuits and Systems for High-Speed Wireless Communications: Challenges and Design Perspectives, Payam Heydari, 連結
無線通訊系統在終端無須佈線、建置成本降低,同時增加使用者數量,這些是它的優勢。不過無線通訊還有一點是有線通訊無法企及的,就是移動性(mobility),不論是行動通訊、衛星通訊還是車聯網、IoT,只要通信雙方有相對運動,都要求滿足移動性的通訊方式。因此,無線通訊仍是值得深入研究的主題。(當然有線通訊也有其重要性,尤其是硬體間資料傳輸,如 GPU 和 memory 之間的通訊,便是現在非常重要的研究領域)
無線通訊(wireless)和有線通訊(wireline)的物理傳輸介質──傳輸通道,有著非常不一樣的特性。有線通訊使用傳輸線或光纖作為傳輸通道,傳輸線的話要考慮線路阻抗、符號間干擾(頻率響應)、串擾(cross-talk)等問題;無線通訊使用空氣/大氣作為傳輸通道,除了各種反射、散射與繞射等大規模衰減(large-scale fading)效應之外,由於通訊雙方會有相對運動,通道基本上是時變的(time variant),還要考慮Doppler shift、delay spread和angle spread等問題,是為小規模衰減(small-scale fading)。無線通訊的通道比起有線通訊,挑戰更巨大。
接著我們就來討論無線通道面臨的兩大挑戰:large-scale fading 及 small-scale fading。
Large-Scale Fading
Large-scale fading,也就是無線通道大尺度的特性。怎樣算是large-scale?這和載波頻率有關,載波頻率為800 MHz的訊號,波長約為37.5公分,large-scale的範圍就會在幾十至幾百個波長,約幾公尺以外。以載波頻率為2.4 GHz的WiFi訊號為例,在同一個房間的訊號強度差不多,但是在同一層樓不同房間(受到阻礙)、或是不同層樓(傳輸距離增加),訊號強度就會有明顯差異。
造成large-scale fading的原因為傳輸訊號的反射、繞射與散射,以及與傳輸距離相關的損耗,建立模型時,通常以path loss和shadowing來描述。下面就來介紹這些因素。
Free space path loss
假設一個點波源,在半徑 $r$ 處波的功率減少程度和 $1/r^2$ 成正比,這是蠻直覺的想法。Friis free space equation便說明free space裡接收訊號功率和Tx-Rx距離的關係:
$$
P_r(d) = \frac{P_t G_t G_r \lambda^2}{(4\pi)^2 d^2 L}
$$
其中 $G_t$ 為Tx天線增益,$G_r$ 為Rx天線增益,$L$ 是system loss factor,$d$ 則是Tx-Rx距離。$P_r(d)$ 很好用,不過更好用的是path loss:
$$
PL (dB) = 10\log{\frac{P_t}{P_r}} = -10\log{\frac{\lambda^2}{(4\pi)^2 d^2}}
$$
當中去除掉天線和系統的參數(如 $L$)。Path loss表示訊號傳播過程中遭受的損耗,並且以dB來表示,在link budget的計算中相當好用。
不過Friis free space equation也不是萬用的,它的前提是Rx位於Tx的遠場,和Tx距離必須大於Fraunhofer distance $d_f$,並且
$$
\begin{align}
d_f &= \frac{2D^2}{\lambda} \\
d_f &\gg D \\
d_f &\gg \lambda
\end{align}
$$
其中 $D$ 是天線外型上最大的長度。上述的path loss也有一個致命的缺點:在 $d = 0$ 時不能用!所以通常會以一個參考點 $d_0$ 作為基準:
$$
PL(d) (dB) = PL(d_0) - 20\log{\frac{d_0}{d}}
$$
反射
反射很容易理解,就是電磁波打到平滑表面產生的現象。下面這張圖表示電場偏振方向平行於入射平面的case,其中 $\epsilon$ 為permittivity,$\mu$ 為permeability,$\sigma$ 為conductance,反射係數可以表示為:
$$
\Gamma_{\parallel} = \frac{E_r}{E_i} = \frac{\eta_2 \sin{\theta_t} - \eta_1 \sin{\theta_i}}{\eta_2 \sin{\theta_t} + \eta_1 \sin{\theta_i}}
$$
其中 $\eta_i = \sqrt{\mu_i/\epsilon_i}$ 為intrinsic impedance。若表面為介電質,則還有不反射的情況,即當入射角等於Brewster angle的時候。
圖片來源:自己,改自[2]。
第二個case中,電場偏振方向垂直於入射平面(見下圖),其反射係數可以表示為:
$$
\Gamma_{\perp} = \frac{E_r}{E_i} = \frac{\eta_2 \sin{\theta_i} - \eta_1 \sin{\theta_t}}{\eta_2 \sin{\theta_i} + \eta_1 \sin{\theta_t}}
$$
當表面為perfect conductor時,$\Gamma_{\parallel} = 1$ 且 $\Gamma_{\perp} = -1$。
圖片來源:自己,改自[2]。
基於這些概念,可以建立ground reflection model,又稱作two-ray model。Two-ray model假設接收到的電場是LOS的成分加上從地面反射而來的成分,$E_{TOT} = E_{LOS} + E_g$。經過一番推導(詳細推論請見[2],假設電場偏振方向為case 2,且入射角趨近於0),得到
$$
\lvert E_{TOT}(d)\rvert = 2\frac{E_0 d_0}{d}\sin{(\frac{\theta_{\Delta}}{2})}
$$
其中 $\theta_{\Delta}$ 為兩條路徑長度差造成的相位差,$\theta_{\Delta} = 2\pi \Delta/\lambda$。這條式子說明僅僅反射就造成free space path loss之外的訊號強度波動,因此有必要將large-scale fading的模型加入隨機性(即shadowing)。
繞射
繞射的概念如下圖,knife-edge diffraction geometry,假設一個刃鋒形的障礙物,寬度為無限寬(出紙面)。
從這張圖片可以計算LOS和經過繞射的兩條路徑長度差:
$$
\Delta \approx \frac{h^2}{2} \frac{(d_1 + d_2)}{d_1 d_2}
$$
以及相位差 $\phi = 2\pi\Delta/\lambda$。如果我們定義Fresnel-Kirchoff diffraction parameter $\nu$ 為
$$
\nu = h\sqrt{\frac{2(d_1 + d_2)}{\lambda d_1 d_2}}
$$
則相位差可以表示為 $\phi = \pi\nu^2/2$。當距離差為 $\lambda/2$,也就是相位差為 $\pi$ 時,LOS和經過繞射的成分疊加起來,會產生破壞性干涉(接收到的訊號振幅為零);同樣的,當距離差為 $\lambda$ 時,會產生建設性干涉(接收到的訊號振幅為兩倍)。由此,我們建立Fresnel zone的概念:Fresnel zone用來表示障礙物位置對繞射訊號強度的影響。第n個Fresnel zone circle的半徑可以表示為(假設 $d_1, d_2 \gg r_n$):
$$
r_n \approx \sqrt{\frac{n\lambda d_1 d_2}{d_1 + d_2}}
$$
這個半徑 $r_n$ 和Tx與Rx距離、障礙物位置(圖中藍色平面位置)有關。此外,同心圓的Fresnel zone形狀是在平面上的投影,實際上的Fresnel zone為橢球體。那麼已知障礙物的位置與形狀,如何得到diffraction zone裡Rx的接收訊號強度呢?一樣假設knife-edge diffraction model,透過計算Fresnel integral,最後整理出下面的式子:
$$
G_d(dB) = 20\log{\lvert F(\nu)\rvert}
$$
$G_d$ 為相對於LOS的訊號強度,所以也可以說是diffraction gain。$F(\nu)$ 為Fresnel integral,可以查表。結論是當 $\nu > 0$ 時,$\nu$ 愈大,diffraction loss愈大,符合直覺。
散射
散射的概念與反射相似,但是反射發生在平滑表面,而散射發生在粗糙平面。平面是否粗糙,可以由Rayleigh criterion來決定:
$$
h_c = \frac{\lambda}{8 \sin{\theta_i}}
$$
其中 $\theta_i$ 是入射角,$h_c$ 則定義為critical height,當表面的凹凸大於critical height,就可以視為粗糙表面。粗糙表面造成的散射,以反射係數的修正來表示:
$$
\Gamma_{rough} = \rho_s \Gamma
$$
其中 $\rho_s$ 為scattering loss factor。還有一種模型叫做radar cross section model (RCS),描述的是「對著Rx散射過來的訊號功率密度」和「打在散射物體上的訊號功率密度」的比值,單位為平方公尺,那這個就不多說。
經典的large-scale model
最經典的large-scale model要屬log-normal shadowing模型。剛才提到large-scale propagation會碰到反射、繞射與散射等等現象,而這些現象又和Tx、Rx所處環境密切相關,不同環境會有不同的shadowing效果。為了方便分析與模擬,科學家提出更一般的模型──log-normal shadowing model,如下:
$$
PL(d) (dB) = \overline{PL}(d_0) + 10n\log{\frac{d}{d_0}} + X_{\sigma}
$$
其中 $X_{\sigma} \sim N(0, \sigma^2)$。可以見得,這個模型不再假設接收訊號的功率和距離平方成反比,而是將exponent設為n;實證資料顯示,在free space n = 2,但是在都會區n = 2.7 ~ 3.5,換句話說,不同的環境也會指示出不同的n。這個模型有兩個參數,n 和 $\sigma$,其中 $\sigma$ 代表shadowing的隨機性,因此可以將某環境下量測到的 $PL(d)$ 作為資料,以線性回歸(with least-squares method)的方式得出 n 和 $\sigma$。
不過這個模型也有缺點,就是 n 和 $\sigma$ 是透過data fitting得到,沒有明確的理論依據。關於log-normal shadowing的其他探討,可以參考這篇文章。
也有許多人提出其他的large-scale model,像是有名的Okumura/Hata model,[1]的作者說明得相當清楚,請參考[1]。其他像是Walfisch and Bertoni model,以及indoor propagation models,這裡就不介紹。
Small-Scale Fading
Small-scale fading,即無線通道小尺度的特性。怎樣算是small-scale?和large-scale一樣,也是由載波頻率決定。比如說,載波頻率2.4 GHz的WiFi訊號,數個波長以內、約一公尺以內的範圍,訊號的變化可以用small-scale fading來解釋。
無線通訊、尤其是行動通訊中,通道是時變的,因此也要考慮時域(time domain)的尺度,一般而言是在數毫秒至數秒,可以用small-scale fading來分析。Delay spread、Doppler spread、angle spread經常拿來描述通道多路徑(multipath)效應,以及建立模型。下面就來介紹。
Delay Spread
在行動通訊中,通道為時變的。因此,以 $h(\tau, t)$ 表示通道的impulse response。經過通道的訊號可以表示為
$$
y(t) = \int_{-\infty}^{\infty}{x(t - \tau) h(\tau, t) \rm d \tau}
$$
顯然這不是常見的convolution。式子中,$t$ 表示當下時間(Rx位置),$\tau$ 表示延遲。因此 $h(\tau, t)$ 表示在時間 $t$ 對 $\delta(t - \tau)$ 的通道響應。若我們將這個impulse response離散化(discretized),劃分為N個bin表示N個路徑,則可以表示為
$$
h(\tau, t) = \sum_{i = 0}^{N - 1}{a_i(t) e^{j\theta_i(t)} \delta(\tau - \tau_i(t))}
$$
其中 $\tau_i(t)$ 就是第i條路徑的延遲,延遲本身也是時變的。這個model需要注意delay bins的size,delay bin間隔太大,則一個bin裡可能包含數條路徑的延遲,模型就不準確;delay bin間隔太小,則可能有部分的bin不包含任何路徑延遲。Delay bin的數目(路徑數目)也需要斟酌。
圖片來源:Wireless Communications: Principles and Practice,T. S. Rapapport,Fig 5.4。
用來描述time delay的統計量有很多,包括平均值(mean excess delay)、標準差(rms delay spread)、比峰值小X dB的delay(excess delay spread),使用power delay profile (PDP)作為機率分布來計算。其中rms delay spread特別重要,因為它和coherence bandwidth有著(相近於)反比的關係。
$$
B_c \approx \frac{1}{5\sigma_{rms}}
$$
Coherence bandwidth ($B_c$)象徵通道的頻率響應,在頻域的變動率(rate of variation)。如果 $B_c$ 很小,表示通道的頻率響應在很小的頻寬內便有大幅度的變動,這時候如果傳輸訊號的頻寬大於 $B_c$,則訊號會產生失真(distortion);反之,訊號各頻率成份受到通道的影響是一樣的,就比較不會有失真的問題。此為通道的time dispersion特性。
Doppler Spread
在行動通訊中,當Rx和Tx有相對移動時,會發生都卜勒效應。當Rx以速率 $v$ 經過Tx,並且和Tx夾角為 $\theta$,則瞬間的Doppler shift為
$$
f_d = \frac{v}{\lambda}\cos{\theta}
$$
其中 $\lambda$ 為載波頻率的倒數,即載波波長。這是單一入射弦波的例子,實際上受到多路徑及速率變化的影響,即使傳送的是弦波,接收到的訊號也不會只是頻率位移,而是會在頻譜上散開來──像是在吐司上塗抹果醬一樣,稱為Doppler spread。經典的Doppler spectrum如Clarke’s model,後面會簡單介紹。
Doppler spread的最大頻率偏移──即 $f_m$ (上式中的 $f_d$)特別重要,因為它和coherence time有著(近似於)反比的關係。
$$
T_c \approx \frac{0.423}{f_m}
$$
Coherence time($T_c$)象徵著通道的實變特性。在 $T_c$ 以內的時間裡,通道的impulse response基本上沒有變化,可以視為time-invariant,因此若傳輸訊號的符號長度(symbol duration)小於 $T_c$,則訊號較不會失真;反之,若符號長度大於 $T_c$,則符號的前半段和後半段看到的impulse response不一樣,就會產生失真。此為通道的frequency dispersion特性。
事實上,coherence bandwidth和coherence time是從其他函數衍生而來的參數,這些函數是頻率響應的autocorrelation、Doppler spectrum的inverse Fourier transform等等,之後有機會再來詳細說明。
Angle Spread
這部分還沒讀好。
small-scale fading channel分類
從time dispersion和frequency dispersion來看,可以將通道分為四種,如下圖所示。
其中 $T_s$ 為訊號的symbol duratoin,$B_s$ 為訊號頻寬,$B_D$ 是Doppler spread的最大頻寬,其實也就是 $f_m$。其他系統參數和之前提到的一樣。這四類當中,最好的就是左下角那個,flat & slow fading,因為可以近似於time-invariant系統,頻率響應又更接近impulse function──也就是說,$h(t) \approx A\delta(t - t_0)$,最接近理想系統。最糟的應該就是右下角的,freq-selective & fast fading,通道隨時都在變化,再加上各種延遲來亂。
經典的small-scale model
Clarke’s model & Jake’s model
Clarke’s model的假設是這樣的:Rx沿一直線等速前進,速率為 $v$。打出一個弦波,載波頻率為 $f_c$,經過散射後,訊號從四面八方、各個角度抵達Rx。收到的訊號(電場強度)可能長得如下式:
$$
E(t) = E_0 \sum_{n = 1}^{N}{C_n \cos{(2\pi f_c t + 2\pi f_n t + \phi_n)}}
$$其中 $\phi_n$ 為(uniform) random phase,$C_n$ 也是隨機變數。$f_n$ 則是不同角度所導致的Doppler shift。上述的帶通隨機過程可以用低通隨機過程來表示:
$$
\begin{align}
T_i(t) = E_0 \sum_{n = 1}^{N}{C_n \cos{(2\pi f_n t + \phi_n)}} \\
T_q(t) = E_0 \sum_{n = 1}^{N}{C_n \sin{(2\pi f_n t + \phi_n)}}
\end{align}
$$(複習lowpass equivalent的概念)。當N非常大,$T_i(t)$ 和 $T_q(t)$ 便會近似於Gaussian random process(參考中央極限定理)。這個random process的PSD就是那個經典的Doppler spectrum,數學表示式如下。
$$
S_D(f) \propto \frac{1}{f_m\sqrt{1 - (\frac{f - f_c}{f_m})^2}}
$$如下圖,可以看到這個頻譜在載波頻率附近「塗抹」散開,並且在 $f_c - f_m$ 和 $f_c + f_m$ 兩處無窮大。時域方面,這個random process的in-phase component ($T_i(t)$)和quadrature component ($T_q(t)$)為獨立的Gaussian process,因此其envelope為Rayleigh distributed,即Rayleigh fading。
經典的Doppler spectrum,$f_m$ = 50 Hz。圖片來源:自己。
Jake’s model則嘗試將Clarke’s model簡化成可以寫成程式的描述,比如說將合成的弦波數目減到最少,合併相同頻率的弦波等等。Jake’s model將此低通訊號如下表示;
$$
\begin{align}
X_i(t) &= 2\sum_{n = 1}^{N_0}{\cos{\beta_n}\cos{\omega_n t}} + \sqrt{2}\cos{\alpha}\cos{\omega_m t} \\
X_q(t) &= 2\sum_{n = 1}^{N_0}{\sin{\beta_n}\cos{\omega_n t}} + \sqrt{2}\sin{\alpha}\cos{\omega_m t}
\end{align}
$$藉由適當的參數設定($\alpha$ 及 $\beta_n$),合成出來的低通訊號和Clarke’s model的低通隨機過程有著類似的頻譜及統計特性(如time-average variance和time-average correlation)。下圖為MATLAB模擬Jake’s model跑出來的fading gain,就是相當經典的Rayleigh fading channel gain。
圖片來源:自己。
結語
第一篇到此為止。目前的寫作風格,是寫給未來失憶的自己,所以脈絡和邏輯都必須寫清楚。但是這樣一來寫作時間拉長,性質也更像是教學而不是筆記。希望能漸入佳境。
參考資料
[1] otto185,HackMD公開筆記,無線通訊之通道選擇與使用1 - 通道介紹
[2] T. S. Rappaport, Wireless Communications : Principles and Practice.